Vargas Licla Jordy || Lenguaje de Programación I: EVAP. 4

Esfuerzo – Deformación

Objetivos:

- Dar a conocer la importancia del esfuerzo y deformación.

- Que todo el alumnado pueda comprender y realizar cálculos de esfuerzo y deformaciones.

Marco Teórico:

ESFUERZO Y DEFORMACIÓN

La mecánica de materiales es una rama de la mecánica que estudia las relaciones entre las cargas externas aplicadas a un cuerpo deformable y la intensidad de las fuerzas internas que actúan dentro de él. El objeto de estudio de la mecánica de materiales es proporcionar al estudiante un conocimiento de la relación entre las fuerzas exteriores aplicadas a una estructura de ingeniería y el comportamiento resultante de los miembros de la misma. La mecánica proporciona la base para el diseño en ingeniería. El origen de la mecánica de materiales data de principios del siglo XVII. Personajes como Leonardo Da Vinci y Galileo Galilei efectuaron experimentos para determinar la resistencia de alambres, barras y vigas, aunque no formularon teorías adecuadas para explicar los resultados de sus pruebas. Debido a que sus investigaciones se basaron en aplicaciones de la mecánica a los cuerpos materiales, llamaron a este estudio “resistencia de materiales”. Sin embargo, hoy en día llamamos a la misma “mecánica de los cuerpos deformables” o, simplemente, “mecánica de materiales”.

Fuerza se define como una interacción entre dos cuerpos; es una cantidad física vectorial que se describe mediante los conceptos intuitivos de “empujar” y “jalar”. Desde el punto de vista de la Dinámica, cuando se aplica una fuerza a un cuerpo, el efecto que tiene dicha fuerza es darle al cuerpo una aceleración y, por tanto, cambiar el estado de reposo o de movimiento uniforme que tenía el cuerpo antes de la aplicación de la fuerza. Esto viene descrito por la Segunda Ley de Newton.

En el ámbito de la Mecánica de los Medios Continuos, lo que nos interesa es el comportamiento que tiene la materia cuando se le aplica una fuerza. En este contexto, el efecto que tiene una fuerza aplicada sobre un determinado cuerpo es la deformación del mismo.

Para estudiar cómo se producen las deformaciones, debemos centrarnos primero en entender que la acción de la fuerza aplicada y el efecto producido dependerán directamente del área sobre la que está actuando la fuerza. Este efecto se denomina esfuerzo, se define como “fuerza por unidad de área” y lo vamos a representar por s.

Por ejemplo, se tiene un área A sobre la que se aplica una fuerza de magnitud F1y se tiene la misma área A pero ahora se le aplica otra fuerza de magnitud F2, mayor que F1, como se indica la figura. ¿Cuál de las dos fuerzas ejercerá un mayor esfuerzo sobre A? La respuesta correcta es F2.

Ahora se tiene un área A1 sobre la que está actuando una fuerza de magnitud F y se tiene la misma fuerza pero ahora actuando sobre otra área A2 mayor que la primera. ¿En cuál de los dos casos descritos se está realizando un mayor esfuerzo? En este caso la misma fuerza ejerce un mayor esfuerzo sobre el área más pequeña, A1.

Matemáticamente, las relaciones anteriores entre fuerza, área y esfuerzo se pueden resumir por la expresión:

o bien :

Esfuerzo:

Las fuerzas internas de un elemento están ubicadas dentro del material por lo que se distribuyen en toda el área; justamente se denomina esfuerzo a la fuerza por unidad de área, la cual se denota con la letra griega sigma (σ) y es un parámetro que permite comparar la resistencia de dos materiales, ya que establece una base común de referencia.

σ = P / A

Donde: P = Fuerza axial;

A = Área de la sección transversal

Cabe destacar que la fuerza empleada en la ec. 1 debe ser perpendicular al área analizada y aplicada en el centroide del área para así tener un valor de σ constante que se distribuye uniformemente en el área aplicada. La ec. 1 no es válida para los otros tipos de fuerzas internas1; existe otro tipo de ecuación que determine el esfuerzo para las otras fuerzas, ya que los esfuerzos se distribuyen de otra forma.

Deformación:

La resistencia del material no es el único parámetro que debe utilizarse al diseñar o analizar una estructura; controlar las deformaciones para que la estructura cumpla con el propósito para el cual se diseñó tiene la misma o mayor importancia. El análisis de las deformaciones se relaciona con los cambios en la forma de la estructura que generan las cargas aplicadas.

Una barra sometida a una fuerza axial de tracción aumentara su longitud inicial; se puede observar que bajo la misma carga pero con una longitud mayor este aumento o alargamiento se incrementará también. Por ello definir la deformación (ε) como el cociente entre el alargamiento δ y la longitud inicial L, indica que sobre la barra la deformación es la misma porque si aumenta L también aumentaría δ. Matemáticamente la deformación sería:

ε = δ/L

En ingeniería, la deformación de un cuerpo se especifica usando los conceptos de deformación unitaria normal y por esfuerzo cortante. Cuando se aplica una fuerza a un cuerpo, ésta tiende a cambiar la forma y tamaño del cuerpo. A esos cambios se les llama deformación y ésta puede ser visible o prácticamente inadvertida si no se emplea el equipo apropiado para hacer mediciones precisas. Por ejemplo, una banda de hule experimentará una deformación muy grande cuando se estira. En cambio, en un edificio sólo ocurrirán deformaciones ligeras en sus miembros estructurales debido a la carga de sus ocupantes. Un cuerpo también puede deformarse cuando la temperatura del cuerpo cambia. Un ejemplo común es la expansión o la contracción térmica de un techo causada por el clima.

Alargamiento normal de un elemento:

& = Lf - Li

& = alargamiento normal de un elemento
Lf = Longitud final del elemento
Li = Longitud inicial del elemento

DIAGRAMA ESFUERZO - DEFORMACIÓN

El diseño de elementos estructurales implica determinar la resistencia y rigidez del material estructural, estas propiedades se pueden relacionar si se evalúa una barra sometida a una fuerza axial para la cual se registra simultáneamente la fuerza aplicada y el alargamiento producido. Estos valores permiten determinar el esfuerzo y la deformación que al graficar originan el denominado diagrama de esfuerzo y deformación.

Los diagramas son similares si se trata del mismo material y de manera general permite agrupar los materiales dentro de dos categorías con propiedades afines que se denominan materiales dúctiles y materiales frágiles. Los diagramas de materiales dúctiles se caracterizan por ser capaces de resistir grandes deformaciones antes de la rotura, mientras que los frágiles presenta un alargamiento bajo cuando llegan al punto de rotura.

DIAGRAMA

El diagrama es la curva resultante graficada con los valores del esfuerzo y la correspondiente deformación unitaria en el espécimen calculado a partir de los datos de un ensayo de tensión o de compresión.

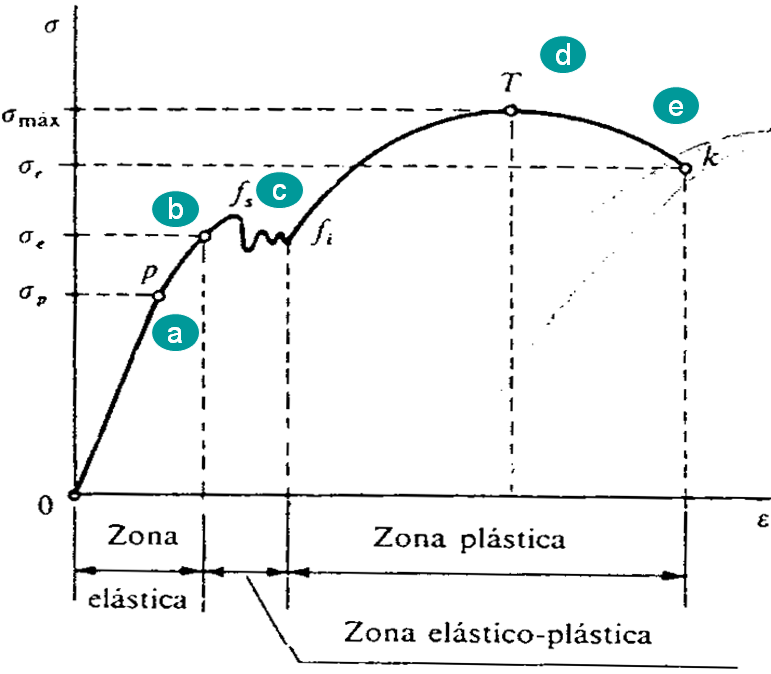
a) Límite de proporcionalidad:

Se observa que va desde el origen O hasta el punto llamado límite de proporcionalidad, es un segmento de recta rectilíneo, de donde se deduce la tan conocida relación de proporcionalidad entre la tensión y la deformación enunciada en el año 1678 por Robert Hooke. Cabe resaltar que, más allá la deformación deja de ser proporcional a la tensión.

b) Limite de elasticidad o limite elástico:

Es la tensión más allá del cual el material no recupera totalmente su forma original al ser descargado, sino que queda con una deformación residual llamada deformación permanente.

c) Punto de fluencia:

Es aquel donde en el aparece un considerable alargamiento o fluencia del material sin el correspondiente aumento de carga que, incluso, puede disminuir mientras dura la fluencia. Sin embargo, el fenómeno de la fluencia es característico del acero al carbono, mientras que hay otros tipos de aceros, aleaciones y otros metales y materiales diversos, en los que no manifiesta.

d) Esfuerzo máximo:

Es la máxima ordenada en la curva esfuerzo-deformación.

e) Esfuerzo de Rotura:

Verdadero esfuerzo generado en un material durante la rotura.

LEY DE HOOKE

En física, la ley de elasticidad de Hooke o ley de Hooke, originalmente formulada para casos de estiramiento longitudinal, establece que el alargamiento unitario que experimenta un material elástico es directamente proporcional a la fuerza aplicada sobre el mismo